Stardis
Stardis is a thermal simulation framework for complex 2D and 3D environments, based on new Monte Carlo algorithms built from reformulations of the main heat transfer phenomena: conduction, convection and radiation. A set of cross-recursive algorithms have then been derived, and result in the simulation of "thermal paths" that explore space and time until a boundary condition or an initial condition is found. The key concept here is that heat transfer phenomena are not considered separately but are naturally coupled via the cross-recursion of the various Monte Carlo algorithms.
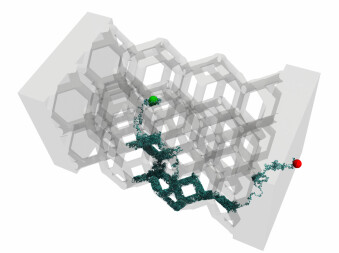
Example of conductive path sampled by Stardis in a foam geometry: it starts from the probe position (green point) and after several diffusive steps reaches a boundary condition (red point).
Beyond its use as a regular thermal simulation tool, the Stardis framework explicitly targets engineers, researcher, teachers or students wishing to fully appropriate the statistical formulation of heat transfer, from theoretical concepts to practical implementation. The complete Stardis framework is thus released under free license that guarantee the users the ability to freely use, study, modify or extend the complete source code according to their needs.
Despite its specific advantages, Stardis is not meant to fully replace already well established and highly validated thermal simulation tools. Instead, it can be seen as an additional tool that can be useful for various purposes:
Probe computation: Stardis will not compute the full temperature field of a system; instead, it can be used to focus on a specific spatial/temporal zone of the system.
Reference method: the numerical uncertainty is a unique feature of stochastic methods. It can be reduced using a reformulation of the underlying integral for specific problems, and possibly using better suited sampling techniques. Ultimately, the numerical uncertainty can also be reduced by increasing the number of statistical samples. Any value of temperature (or flux) computed by Stardis must agree with the values computed by other tools, within the uncertainty range (and also within the limits of validity of the various assumptions used to derive the Monte Carlo algorithms used in Stardis). This can prove very useful in order to validate any result obtained by any thermal solver in a case when no analytic solution is available or when a physical intuition is impossible to achieve due to the complexity of the problem.
Educational purposes: since the various probability sets used by the underlying Monte Carlo algorithms solely rely on the physics, thermal paths naturally explore the spatial and temporal zones of interest in the system. This can be a drawback in some situations (the paths will have a hard time exiting a highly conductive solid surrounded by non-conductive media) but is a major asset for the direct visualization of what contributes to a given result: the main sources of heat, what transfer modes are dominant, what are the main paths of heat transfer, etc.
Sensitivity analysis: the Green functions of the system (estimated and stored during an initial Monte Carlo computation) can be reused for subsequent (very fast) post-processing computations. This makes possible to explore the sensitivity of any given result to the variations of a boundary or initial condition, or internal power source. This technique is only a small part of a family of so-called "symbolic" Monte Carlo algorithms that extend the scope of sensitivity analysis to any thermal parameter (for instance: the conductivity of a given solid, a convective exchange coefficient or the emissivity of a solid).
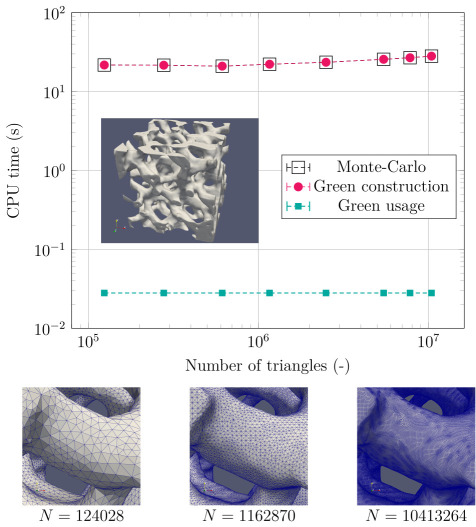
Stardis computation time as function of geometrical refinement. Both the standard Monte Carlo computation and the Green function construction and usage are insensitive. In this example, once constructed, using the Green function with any new set of sources is 10³ times faster than Monte Carlo.
The Stardis framework is structured around two main components. The first one, Stardis-Solver, is the core library that implements the Monte Carlo algorithms. The second one is the Stardis application, a command line tool that can be seen as a reference implementation of a complete workflow relying on Stardis-Solver, from input data describing the system to simulate (geometry, thermal properties, limit conditions, etc.) to heat transfer simulation and results post-processing. See below for more information on each of these components.
Related articles
Caliot et al. 2024, "Coupled heat transfers resolution by Monte Carlo in urban geometry including direct and diffuse solar irradiations", International Journal of Heat and Mass Transfer (open access)
Penazzi et al. 2024, "Path integrals formulations leading to propagator evaluation for coupled linear physics in large geometric models", Computer Physic Communications (open access)
Bati et al. 2023, "Coupling Conduction, Convection and Radiative Transfer in a Single Path-Space: Application to Infrared Rendering", SIGGRAPH (open access)
Tregan et al. 2023, "Coupling radiative, conductive and convective heat-transfers in a single Monte Carlo algorithm: A general theoretical framework for linear situations", PLOS ONE (open access)
Villefranque et al. 2022, "The “teapot in a city”: A paradigm shift in urban climate modeling", Science Advances (open access)
Stardis-Solver
Stardis-Solver is the core library of Stardis: it simulates coupled convecto - conducto - radiative heat transfers by sampling thermal paths that explore space and time until a boundary condition or an initial condition is met. Note that this path formulation does not require any volumetric mesh: in addition of the thermal properties and the limit/boundary conditions, only the geometry defining the contours of the objects is necessary.
The coupled Monte Carlo algorithms implemented into Stardis-Solver are based on the following hypothesis:
Conduction: Stardis-Solver offers two ways of sampling unsteady Brownian motion to solve for conductivity in a solid. The delta sphere algorithm is based on the discrimination of thermal heat transfer in solids, which introduces the notion of conductive path length. Solutions obtained using this algorithm are formally exact to the limit of zero path length. In practice, this path length must be adapted to a given geometrical configuration so that its value is small compared to the smallest typical space-time length of a solid.
As an alternative, the Walk on Sphere algorithm samples an unbiased diffuse trajectory in a solid with Dirichlet boundary conditions, unbiased with respect to what numerical accuracy can account for. Its coupling with other boundary or connection conditions behaves as with the delta sphere algorithm, i.e. the solution is exact when the length of the trajectory used as a first-order approximation tends towards 0.
Convection: fluid media are supposed to be isothermal, even if their temperature may vary with time. This hypothesis relies on the assumption of perfectly agitated fluids.
Radiation: local radiative transfer is solved by an iterative numerical method (Picard algorithm) that requires the knowledge of a reference temperature field. At the basic level (one level of recursion), and using a uniform reference temperature field, this algorithm translates into the hypothesis of a linearized radiative transfer. Using a higher order or recursion makes possible to converge the result closer to the solution of a rigorous spectrally-integrated radiative transfer (a difference of temperatures to the power 4 when integrated over the whole spectrum). The higher the recursion order, the better will be the convergence of the algorithm.
The main functionalities provided by Stardis-Solver upon the aforementioned hypothesis are as follows:
Probe computation: Stardis-Solver computes the temperature at any given position (spatial and temporal). The main idea is that thermal paths start from this probe position, and scatter in space while going back in time, until a (spatial) boundary condition or a (temporal) initial condition is met. In addition to the value of temperature, using a Monte Carlo method makes it possible to compute a numerical uncertainty (standard deviation of the weight distribution) over each result.
Integrated calculation: thanks to Monte Carlo, Stardis-Solver can calculate the temperature of an entire volume or surface, over a given time range, without increasing calculation time or uncertainty compared with a probe-based calculation at a specific point in time.
Flux computation: Stardis-Solver can compute the flux over any surface (or group of surfaces) at any time. Alternatively, it can also compute the total energy output from a solid element where an internal source of power must be taken into account.
Green function: the value of temperature computed at a probe position is no more than the mean of the Monte Carlo weights of a set of thermal paths. In practice: when no internal power source has to be considered, the weight of any given thermal path is the temperature of the boundary or initial condition that has been reached; when internal power sources or imposed fluxes are taken into account, additional contributions to the weight must be continuously evaluated by the thermal conduction algorithm, but these contributions are proportional to the local dissipated power and imposed flux.
In any case, the position and date at the end of each thermal path (and also accumulation coefficients) can be stored during a first complete Monte Carlo simulation. This information, known as the Green function, can then be used in a (very fast) post-processing step to compute all required results for different boundary and initial conditions (and also different internal power sources and imposed flux).
Infrared rendering: Stardis can render a scene in infrared without prior knowledge of the temperature field. Thermal paths that start at the camera in radiative mode propagate through the model, possibly in conductive, convective or radiative mode until reaching a boundary condition (or an initial condition in a non-stationary case).
Temporal dynamics analysis: Stardis-Solver can output the end of each path sampled during a Monte Carlo computation, including position, elapsed time, and boundary/medium ID. This not only allows to weight the contribution of each boundary or initial condition to the result, but also gives the temporal dynamics of these contributions.
- Thermal path visualization: Stardis-Solver can output the complete history of a set of thermal paths for later visualization. In addition to positions and dates, physics data is stored along thermal paths, such as the type of heat transfer phenomenon involved at each step, the accumulated power and flux, etc.
Infrared rendering by Stardis of a city district generated by City_Generator2 from the cadastral map of Ile du Ramier in Toulouse, France. Temperature are given in Kelvin. The coupled exchanges of convection, conduction and radiation are evaluated within and between all buildings, i.e. in each room, through every pane of glass and wall with insulation, via the floor, etc. Note that shadows are "heat" shadows produced by the sun defined as an external source boundary condition.
Stardis CLI tools
The stardis framework includes Command Line Interface (CLI) software, namely stardis and sgreen, to use along with Stardis-Solver. They make it easy to exploit the features of the solver.
stardis: it is the main CLI tool of the Stardis framework. It is a barebone front-end to the stardis solver. Depending on the provided command line arguments, it simulates a thermal system described through a simple text file and geometry files and produces various types of output, from simple Monte Carlo results to infrared images or Green functions. Refer to its manual page for more informations.
sgreen the purpose of
sgreenis to post-process binary green-function files produced bystardis. It allows to apply a set of values to the initial and boundary conditions as well as the power and flux sources of the model to produce the same result a new simulation would produce. The obvious benefit of using thesgreenpost-process instead of a new Monte Carlo simulation is the tremendous improvement on computation time. Refer to its manual page page for more informations.
Infrared timelapse animation of a chip and its heatsink covering a 14-second period of time. Computed using the stardis infrared rendering feature, one image per simulated second.
Installation
The installation of Stardis consists of compiling the solver and the
command line tools directly on the target machine.
A simple way is to rely on
star-build,
which automates the build and installation of stardis and
its dependencies from source code.
Prerequisites
To build stardis with star-build, first make sure your system has
the following prerequisites:
- POSIX shell
- POSIX make
- curl
- git
- mandoc
- pkg-config
- sha512sum
- GNU Compiler Collection in version 8.3 or higher
- OpenMPI library and headers in version 2 or higher (optional)
Build
Assuming that the aforementioned prerequisites are available, the build procedure is summed up to:
~ $ git clone https://gitlab.com/meso-star/star-build.git
~ $ cd star-build
~/star-build $ make \
PREFIX=/path/to/stardis/ \
BUILD=src/therm-apps/stardis_0.12.sh
With PREFIX defining the path where Stardis will be installed
and BUILD defining the installation script to be run.
By default, Stardis is built with MPI enabled, so OpenMPI is one of its
requirements.
To disable MPI support, simply set the DISTRIB_PARALLELISM parameter
to NONE as follows:
~/star-build $ make \
PREFIX=/path/to/stardis/ \
BUILD=src/therm-apps/stardis_0.12.sh \
DISTRIB_PARALLELISM=NONE
Run
Evaluate the installed profile file in the current
shell to register stardis against it.
You can then run stardis and consult its manual pages:
. /path/to/stardis/etc/profile
stardis -h
man stardis
Refer to the Stardis: Starter Pack to quickly run a
thermal simulation through the stardis CLI; this archive provides
input data and scripts and is a good starting point to begin with the
Stardis framework.
License
Stardis is free software released under the GPLv3+ license: GNU GPL version 3 or later. You can freely study, modify or extend it. You are also welcome to redistribute it under certain conditions; refer to the license for details.