Validation
This webpage provides the references to validations of the Stardis code and the theoretical framework it is based on.
We first present validations against analytical model, which are directly provided in Stardis as non-regression tests.
We then refer to scientific papers in which Monte Carlo algorithms are compared to deterministic solvers on non trivial configurations.
Finally, we present a validation test case of SYRTHES, the thermal code developed by Électricité de France, which provides both a finite element solver and a Monte Carlo solver powered by Stardis.
Comparison against analytical results
Stardis provides comparisons against analytical solutions.
These non-regression tests are available in the src/ directory of
Stardis Solver
(denoted by test_*).
Note that the tests are performed on the direct Monte Carlo simulation
and the propagator (path-replay with different conditions) when
possible.
For each test, the scene geometry and
physical parameters are described in the header.
Among these, we note the following tests:
test_sdis_conducto_radiative.c validates the steady resolution of the coupled conduction and radiative transfer in a solid surrounded by two different fluids (left/right faces).
test_sdis_convection_non_uniform.c validates the transient resolution of the convection for a fluid inside a cube with faces of different known temperatures.
test_sdis_transient.c validates the transient resolution of conduction in nested cubes.
test_sdis_solve_boundary.c validates the steady computation of the boundary temperature on a solid cube interfaced with a fluid with known temperature.
test_random_walk_robustness.c validates the random walk in a solid with / without a source term in complex geometry.
Cross-comparison against deterministic solvers
Stardis is also validated against usual deterministic codes, on more complex geometries where no analytical solution exists. We list here the academic papers which include such validations and provide a description of the configuration and mention the code used for comparison.
Penazzi et al., "Path integral formulations leading to propagator evaluation for coupled linear physics in large geometric models", Computer Physics Communications 2024, appendix C.
- Validation against COMSOL
- Solid with fluid cavities
- Coupled conduction, convection (perfectly mixed cavity) and radiation; homogeneous coefficients
- Stationary state
- Validation of the propagator
Ibarrart et al., "Advection, diffusion and linear transport in a single path-sampling Monte-Carlo algorithm: getting insensitive to geometrical refinement", Preprint 2022, figures F.9 and F.10.
- Validation against COMSOL or ANSYS Fluent
- Poiseille duct or Kelvin cells
- Coupled conduction, convection (with advection) and radiative transfer; homogeneous coefficients
- Stationary state
Caliot et al., "Combined conductive-radiative heat transfer analysis in complex geometry using the Monte Carlo method", Eurotherm 2018, figures 6 to 9.
- Validation againsta ANSYS Fluent
- Kelvin cells
- Coupled conduction and radiative transfer
- Stationary state
Retailleau et al, "Résolution d’un problème de transferts thermiques couplés en géométrie urbaine par la méthode Monte Carlo", in SFT 2023, figure 4.
- Validation against finite differences
- Slab with Robin conditions
- Coupled conduction, convection (perfectly mixed cell) and radiative transfer
- Un-stationary state
Stardis in SYRTHES
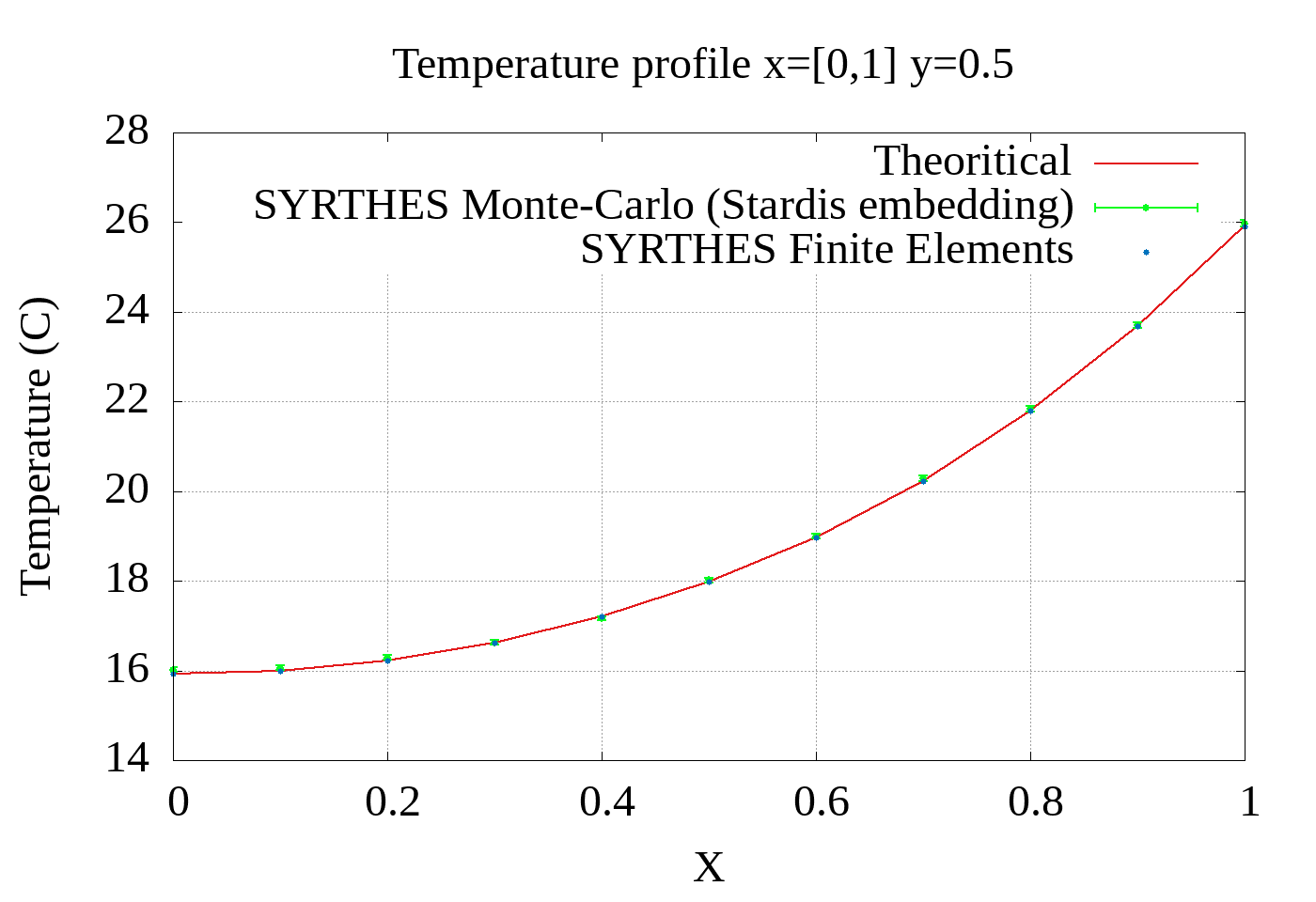
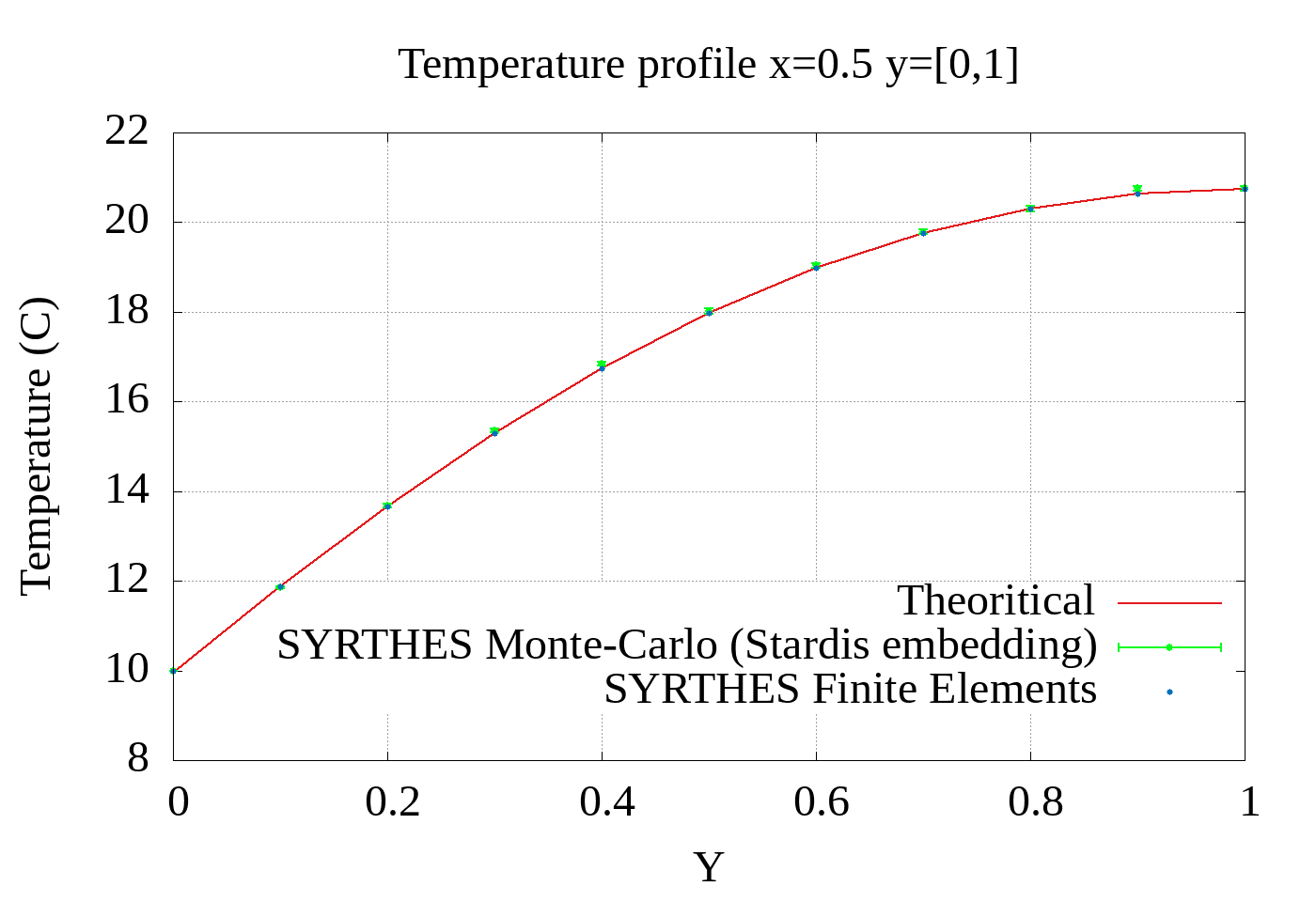
Stardis is used in the SYRTHES code of the French electric company Électricité de France. Both deterministic and stochastic resolutions can therefore be compared on the exact same CAD input. Here we provide the validation on one stationary test case of conduction inside a square. Both the finite elements and the Monte Carlo (using Stardis) resolutions are compared.
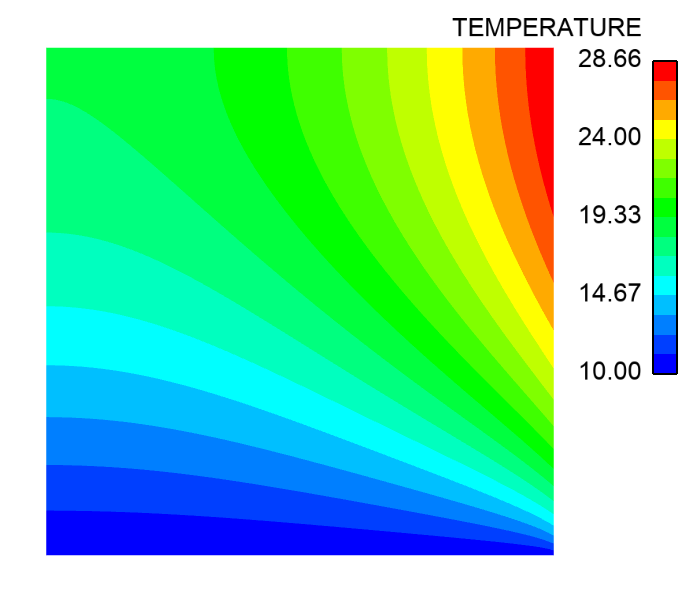
The left figure describes the configuration of the test case. The system to be simulated is a solid square with one edge having a known temperature. Another edge has a convective exchange with a fluid whose temperature is also known. The two other edges are adiabatic. The right image illustrates the temperature field corresponding to this configuration at steady state.
Validation of the Finite element solver and the Monte Carlo solver (i.e. Stardis) of SYRTHES against the analytical solution of the test case presented above. Both curves are computed at steady state at probe positions varying along the X axis (Top) or the Y axis (Bottom).
The version of SYRTHES used for this validation is still on development and available on-demand. Please contact us to obtain this version.